Annual DIMACS REU graph puzzle
Winners!
2025: Jadeep Sidhu and Edward Xiong
2024: Dmitriy Shvydkoy (39 seconds later: Adam Dzavoronok, Jakub Sosovicka, and Tymofii Reizin)
2023: Barbora Dohnalova and Ondrej Sladky
2022: Samuel Hiken
2019: Jan Petr and Jakub Pekarek
2018: Scott Harman
2017: Jakub Pekarek
2016: Thomas Murrills
2025 - 8th annual DIMACS REU graph puzzle
???
2024 - 7th annual DIMACS REU graph puzzle
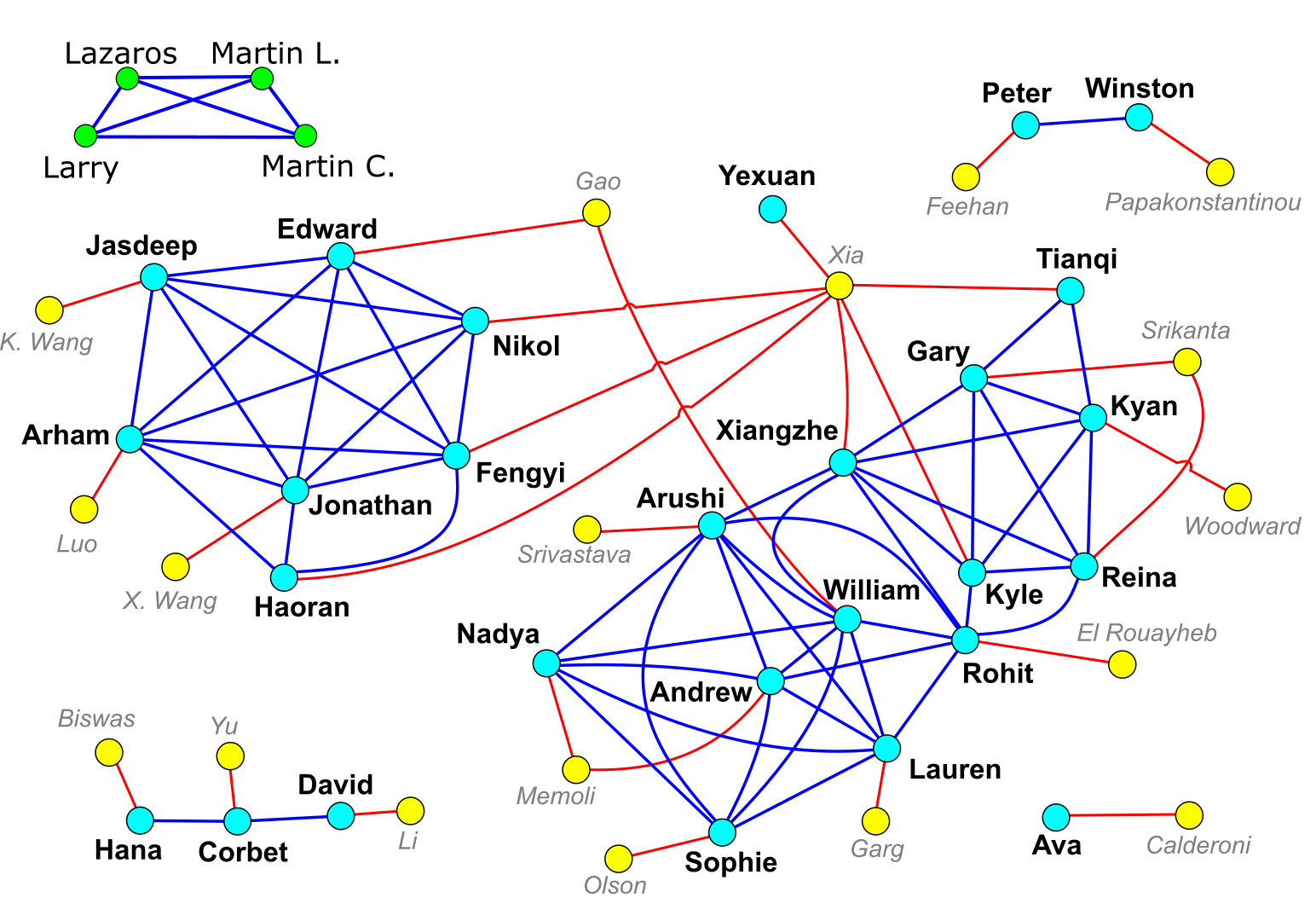
For each name, take the number corresponding to each letter (so A=1, etc), and then find the average over the whole name.
Connect two students if these numbers are within 1 of each other. The thickness of the connection depends on how close two numbers are.
Mentors are simply connected to the students they supervised.
2023 - 6th annual DIMACS REU graph puzzle
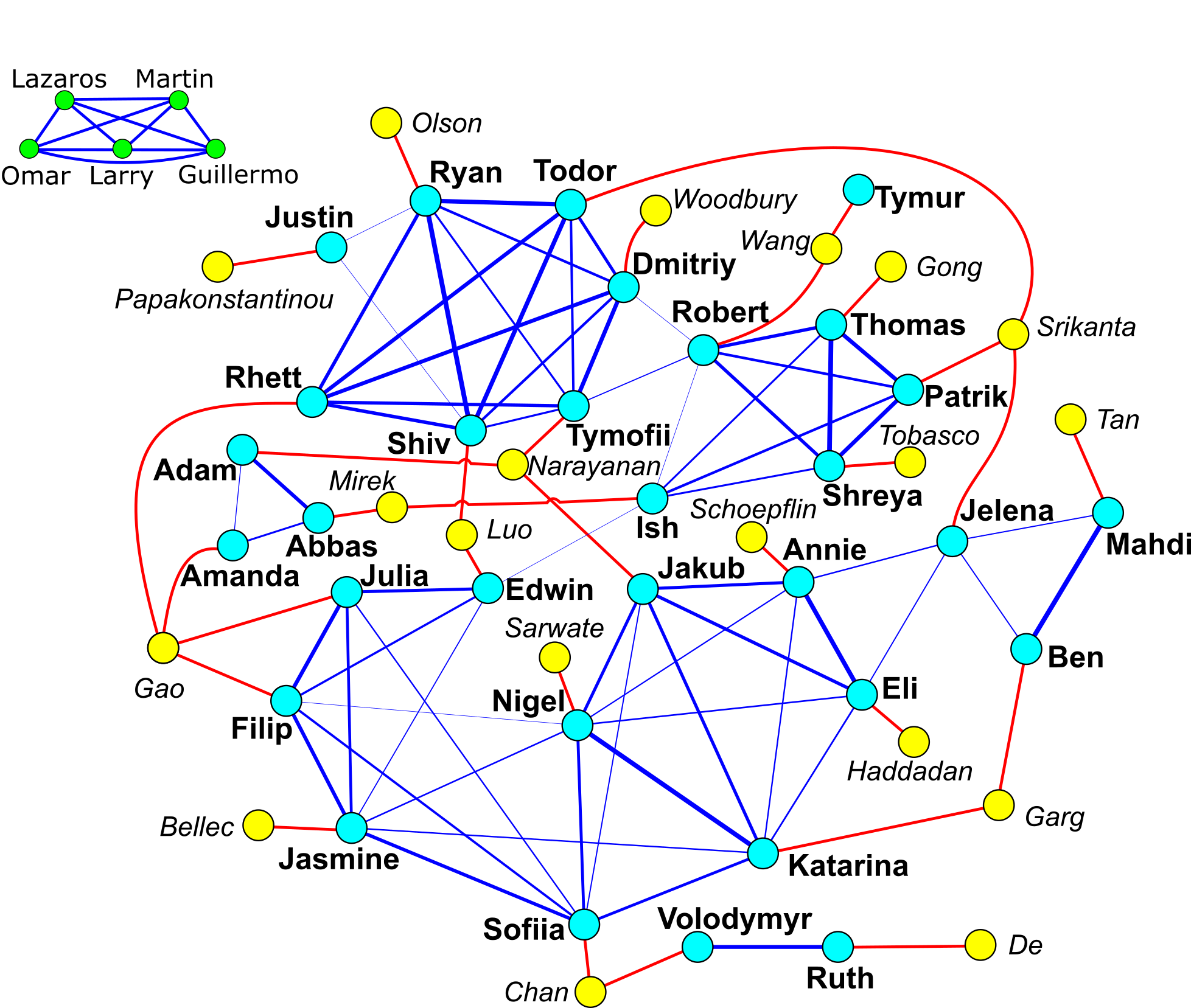
Call z the distance in the alphabet between the first and last letter in a student's first name.
Connect two students with a thick line iff their values of z are the same.
Connect two students with a thin line iff their values of z differ by 1 and their first letter is in the same half of the alphabet.
Mentors are simply connected to the students they supervised.
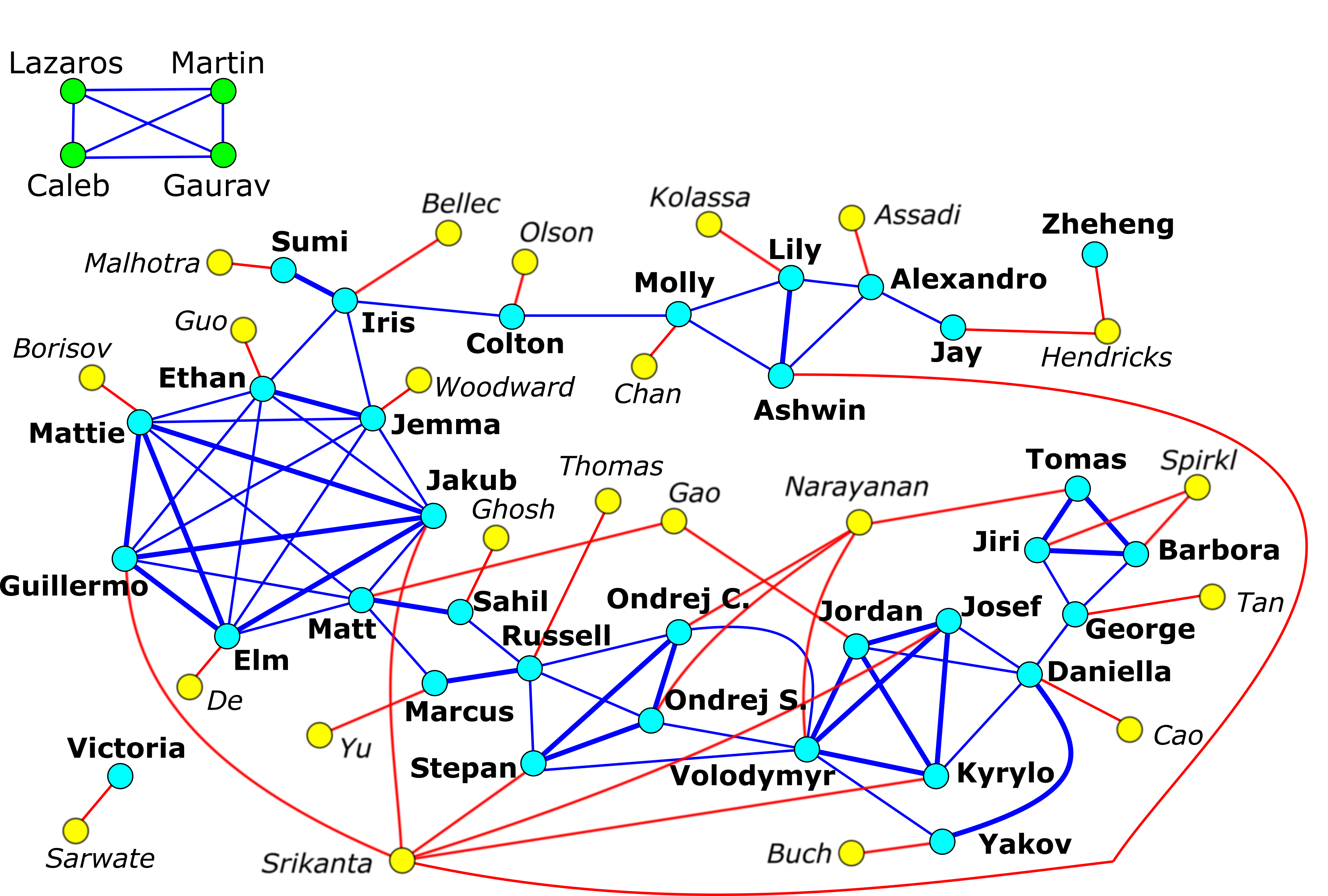
2022 - 5th annual DIMACS REU graph puzzle
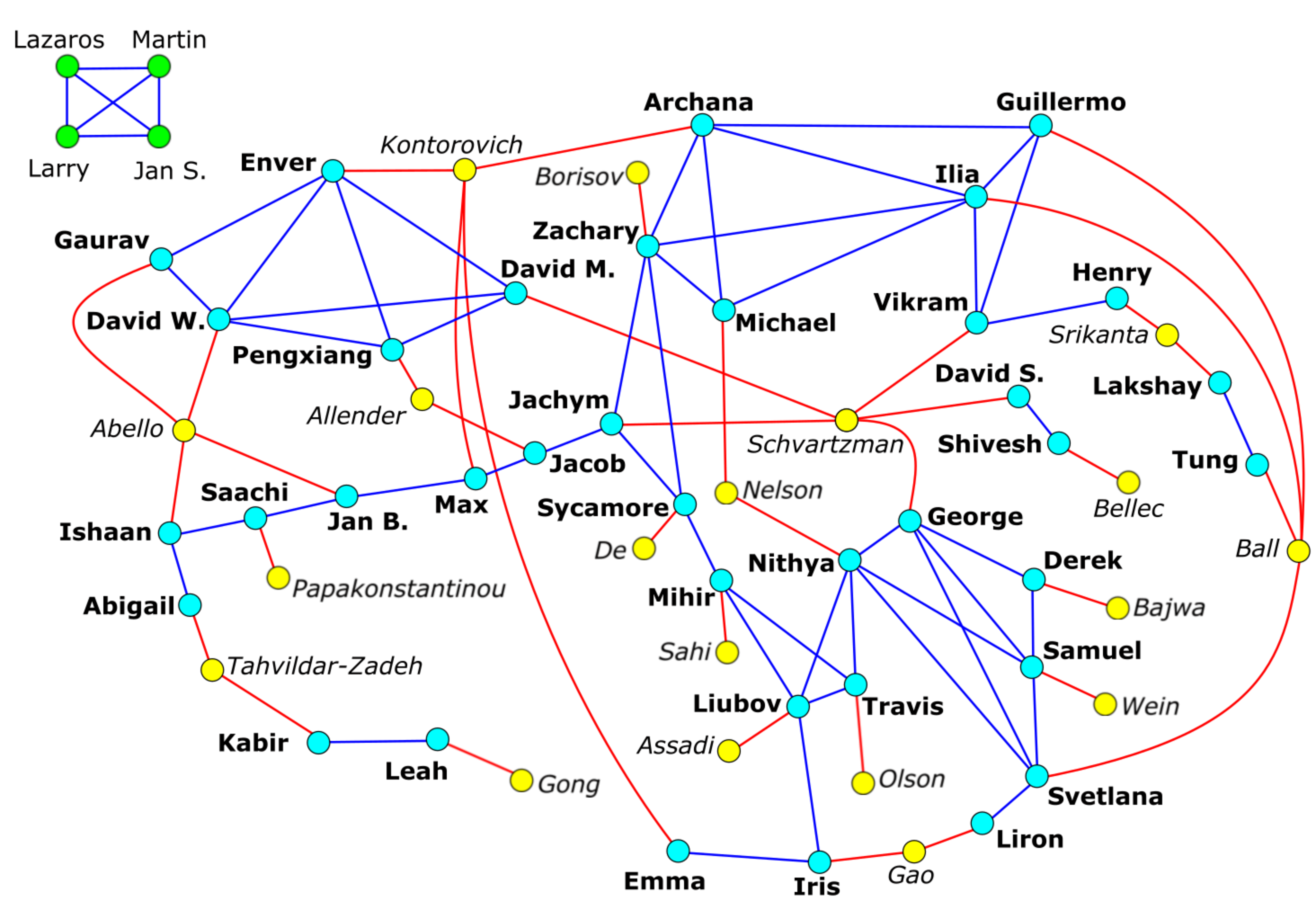
For any letter #, let f(#) be the position of # in the alphabet (ie f('a') = 1, f('b') = 2, etc). If a word w has an odd number of letters with middle letter #, let g(w) = f(#). If w has an even number of letters, with middle letters #_1 and #_2, let g(w) = [f(#_1) + f(#_2)]/2.
Embed a name into 2-dimensional Euclidean space as follows:
x-coordinate = g(first name)
y-coordinate = g(last name)
Any two points within distance 4 are then connected in the graph.
Mentors are simply connected to the students they supervised.
2019 - 4th annual DIMACS REU graph puzzle
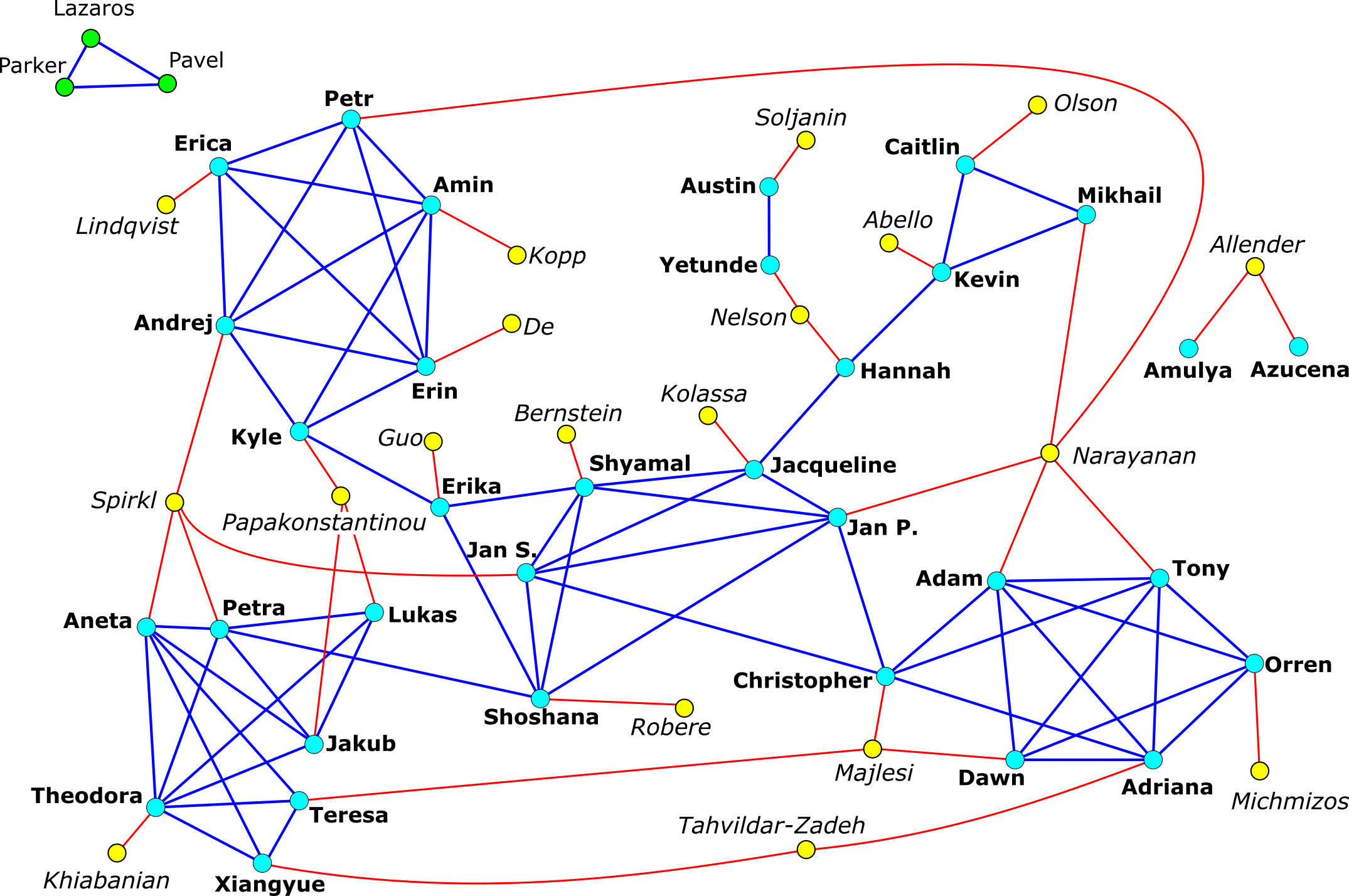
Map each node to a point (x,y) in a Euclidean plane where
x=Distance in the alphabet of the first two letters in student's first name
y=Distance in the alphabet of the last two letters in student's first name
Any two points within distance 4 are then connected in the graph.
Mentors are simply connected to the students they supervised.
2018 - 3rd annual DIMACS REU graph puzzle
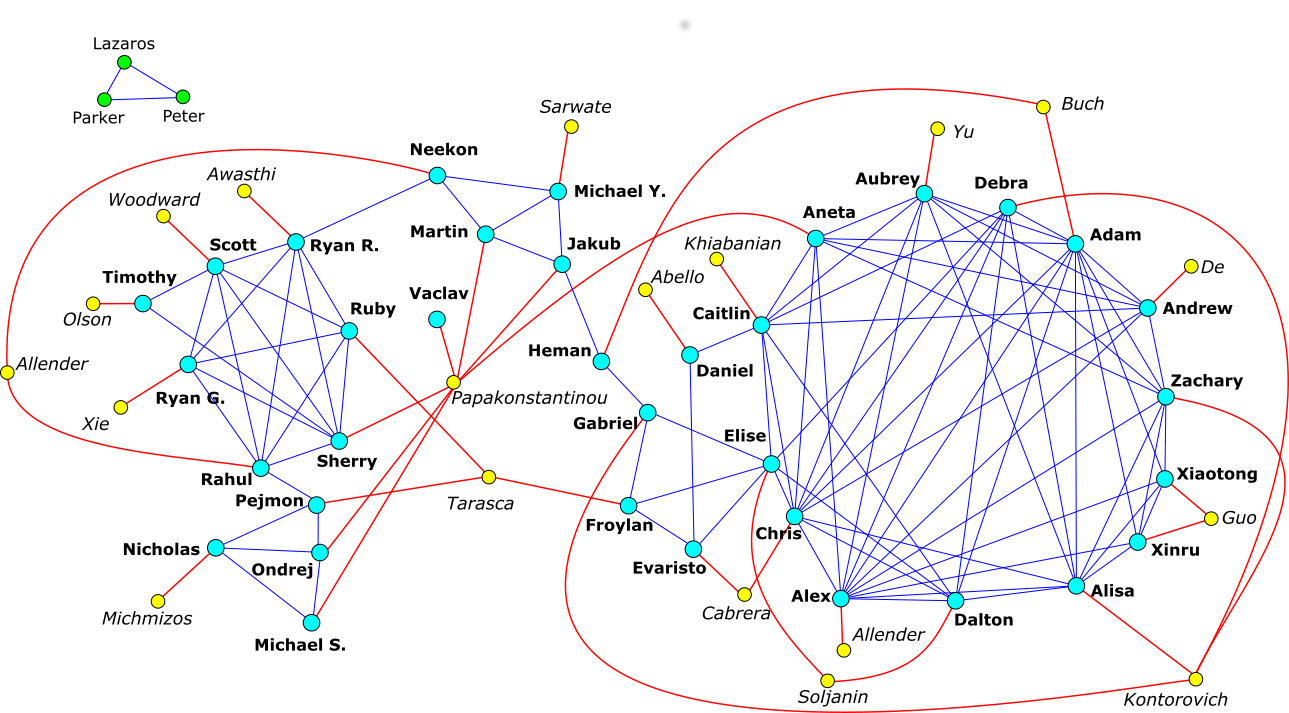
Each student is assigned two variables, r and θ, which correspond to the polar coordinates on a plane:
r = Number of letters in student's last name
θ = (Position in the alphabet of the first letter of the first name)*360/26
[i.e. A=0 degrees, B=1*360/26=13.84 degrees, ... , Z=25*360/26=346.15 degrees.]
Connect two students if their Euclidean distance is smaller than 4.
Mentors are simply connected to the students they supervised.
2017 - 2nd annual DIMACS REU graph puzzle
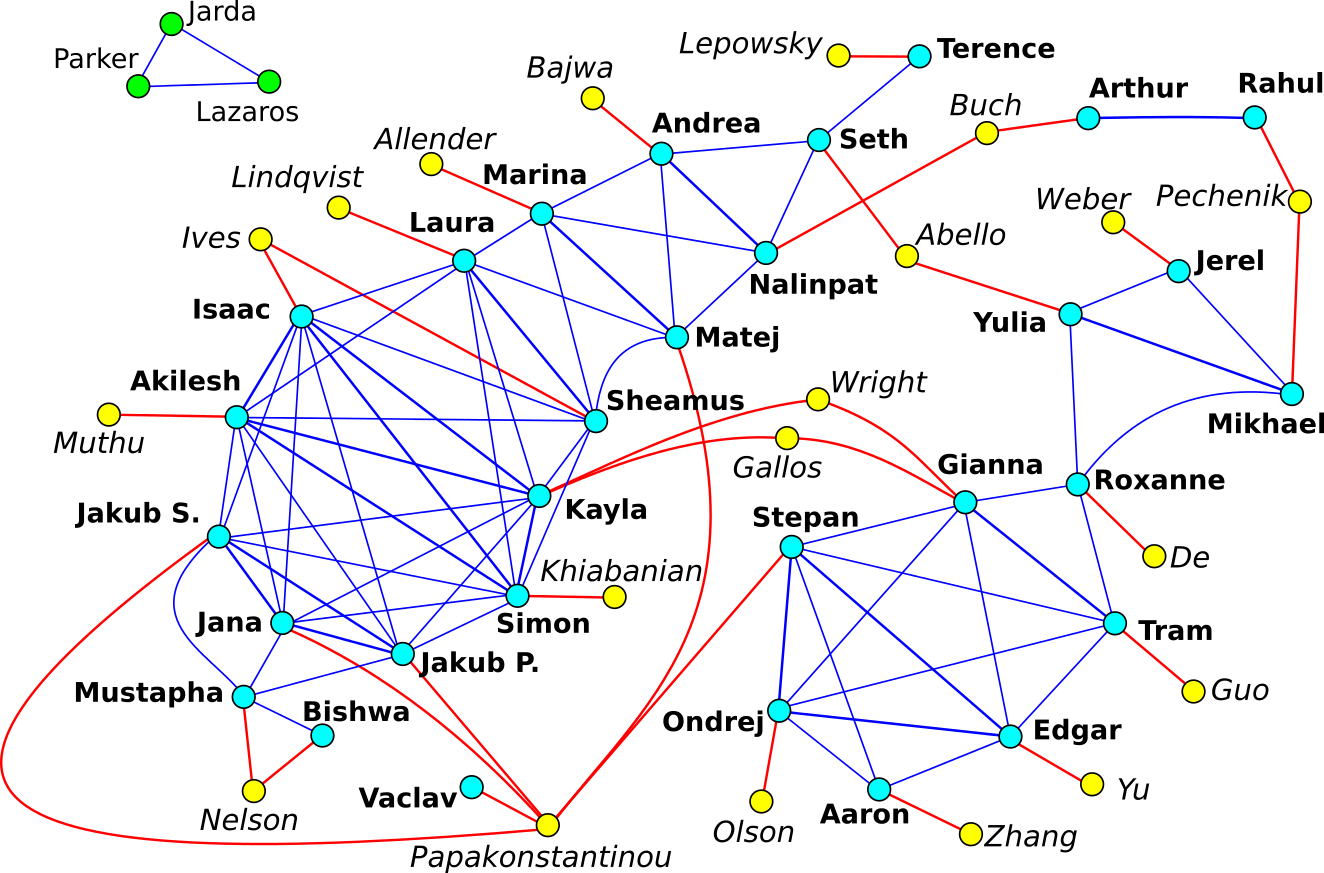
Call Lname the distance in the alphabet between the two first letters in a student's first name
(for example, Aaron has Lname=0 and Edgar has Lname=1).
Connect two students with a thick line if they have the same Lname value
and connect them with a thin line if the difference of their Lname values is 1.
Mentors are simply connected to the students they supervised.
2016 - 1st annual DIMACS REU graph puzzle
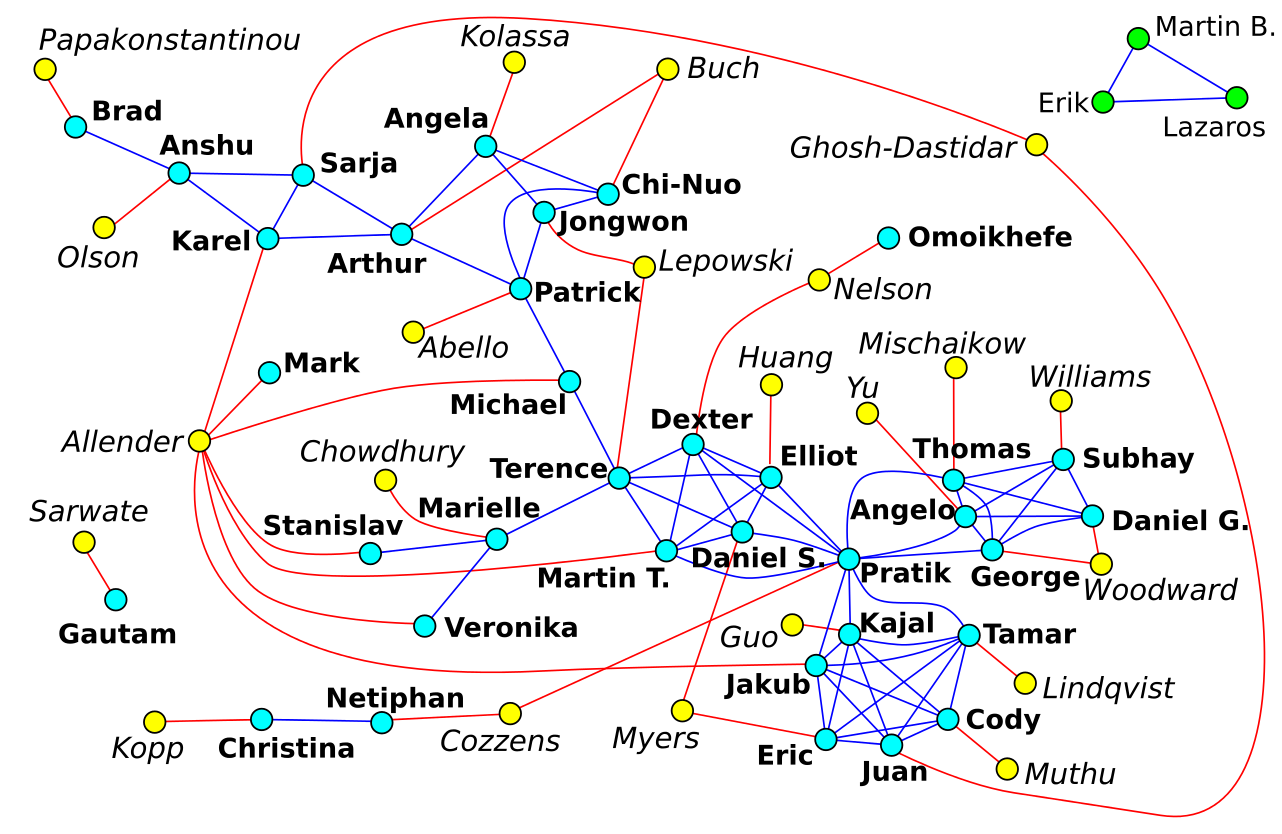
Map each node to a point (x,y) in a Euclidean plane where
x=number of letters in student's first name
y=number of letters in student's last name
Any two points within distance 1 are then connected in the graph.
Mentors are simply connected to the students they supervised.