
2022 DIMACS REU Proposed Project Descriptions
Please revisit this page frequently, since additional projects may be posted through January. Your application, including your preference for the offered projects, can be updated by using the link received after your registration.
The projects are indicative of the research planned by the mentors, but may be modified by the time that the REU starts.
*Note that you must be a U.S. Citizen or Permanent Resident to be eligible for these projects.
Metacomplexity and Non-interactive Zero Knowledge Proofs
Project #: DC2022-01
Mentor: Eric Allender, Computer Science
Abstract: A recent publication (joint with DIMACS REU students) that studied "metacomplexity" (i.e., the computational complexity of showing that problems are hard to compute) resulted in the definition of a new complexity class. This class dealt with a class of problems that have space-bounded non-interactive zero-knowledge proofs. Many basic properties of this complexity class remain unexplored. This project will aim to get a better understanding of this new complexity class.
References:
- Eric Allender, John Gouwar, Shuichi HIrahara, and Caleb Robelle: Cryptographic Hardness under Projections for Time-Bounded Kolmogorov Complexity, Proc. 32nd International Symposium on Algorithms and Computation (ISAAC 2021), pp. 54:1--54:17.
- Eric Allender, Mahdi Cheraghchi, Dimitrios Myrisiotis, Harsha Tirumala, and Ilya Volkovich, One-Way Functions and a Conditional Variant of MKTP, Proc. 41st IARCS Annual Conference on Foundations of Software Technology and Theoretical Computer Science (FSTTCS 2021), pp. 7:1--7:19.
- Eric Allender, Rahul Ilango, Neekon Vafa: The Non-Hardness of Approximating Circuit Size, Proc. 14th International Computer Science Symposium in Russia (CSR 2019), Lecture Notes in Computer Science 11532, pp. 13-24.
- Eric Allender, Joshua Grochow, Dieter van Melkebeek, Cristopher Moore, and Andrew Morgan: Minimum Circuit Size, Graph Isomorphism and Related Problems, SIAM Journal on Computing, Vol. 47(4), 2018, 1339-1372.
- Eric Allender and Shuichi Hirahara: New Insights on the (Non-)Hardness of Circuit Minimization and Related Problems, ACM Transactions on Computation Theory (ToCT), 11,4 (2019) 27:1-27:27.
- Eric Allender, Dhiraj Holden, and Valentine Kabanets: The Minimum Oracle Circuit Size Problem. Computational Complexity 26 (2017) 469-496.
- Eric Allender and Bireswar Das: Zero Knowledge and Circuit Minimization. Information and Computation, 256 (2017) 2-8.
- Michael Rudow: Discrete Logarithm and Minimum Circuit Size, Information Processing Letters 128 (2017) 1-4.
The Cryptography of Deep Nets
Project #: DC2022-02
Mentor: Periklis Papakonstantinou, Management Science and Information Systems
Abstract: Deep Neural Networks are ubiquitous. They have dominated the modern applications of Artificial Intelligence, ranging from medicine and healthcare to self-driving cars and surveillance systems. Every year thousands of research papers are published in the main Machine Learning and Artificial Intelligence venues about deep networks. Despite the bulk of work surprisingly little is known about the correct/certified use of the deep networks. For example, in some mission-critical applications, we would like to know that the deep network one is using has not been modified. If I give you a deep network for you to use, how do I know that when you are using it you haven't modified it? This REU project aims to conceptualize the cryptographic properties of deep networks (for instance, what does it mean mathematically "you haven't modified it when using it") by identifying an appropriate set of specifications and devising protocols that meet these specs.
Prerequisites for this project are mathematical maturity, a class in Cryptography (or *prior* knowledge in Cryptography through self-study) and standard courses in Algorithms and Combinatorics. Ideally, the student has taken a course in Computational Complexity.
Approximation Algorithms for Token Swapping
Project #: DC2022-03
Mentor: Nicole Wein, DIMACS
Abstract: In theoretical computer science, "token swapping" is the following problem. We are given a graph on n vertices and a set of n distinct tokens, where exactly one token is on each vertex. We are also given a desired final configuration of the tokens with exactly one token on each vertex. To get from the initial configuration to the final configuration, we perform a series of "swaps" where each swap exchanges two tokens on adjacent vertices. The goal is to output the minimum number of swaps necessary to reach the final configuration. The token swapping problem is NP-hard.
This project focuses on approximation algorithms for token swapping. There is a known 4-approximation in polynomial time, but is it possible to get a better approximation ratio? Or is there some inherent limitation against getting a better approximation ratio?
Computationally efficient coding schemes for semi-adversarial communication models
Project #: DC2022-04
Mentor: Anand Sarwate, Electrical and Computer Engineering
Abstract: Alice wants to send a message m of k bits to Bob over a communication link by encoding into a codeword x of n>k bits. The communication link is partially controlled by an adversary, Jamie, who wishes to prevent Alice from sending her message. Jamie can erase a total of p n bits so that Bob receives n symbols that are either 0, 1, or "e". How large can we make the communication rate k/n$ while ensuring Bob can decode the message? It turns out the answer depends on what Jamie is allowed to know about the scheme Alice and Bob use and the about the transmitted codeword. For example, they might be able to see the bits one-by-one as they go over the link (an online adversary) or they might be able to see the bits through a noisy measurement device like a wiretap (a myopic adversary). We know how high a rate Alice and Bob can get in many different scenarios, but the codes we need to use are not computationally efficient. This project will look at how to put together several ingredients (algebraic codes, random permutations, hashing, and maybe more) to try and get a computationally efficient scheme to work for one scenario.
Maximal Independent Sets in Graph Streams
Project #: DC2022-05
Mentor: Sepehr Assadi, Computer Science
Abstract: In the graph streaming model, the edges of an input graph G=(V,E) are given to the algorithm as the sequence E=<e1,...,em> one by one in some arbitrary order and the vertex set is fixed to V := {1,...,n}.
A semi-streaming algorithm is allowed to make one or a small number of passes over this sequence of edges
and uses only O(n*polylog(n)) memory (thus if the graph is sufficiently dense, the memory of the algorithm
is smaller than the input stream and so we cannot simply store the input graph).
Given an undirected graph G=(V,E), an independent set in G is any set I⊆V of vertices with no edges
between them. A maximal independent set (MIS) is any independent set I which is not a proper subset of
any other independent set; in other words, for any vertex in the graph not in the MIS, there is at least one
neighbor inside this MIS.
The goal of this project is to design a semi-streaming algorithm for finding an MIS in the graph streaming
model. Currently, it is known that any semi-streaming algorithm for MIS needs strictly more than one pass
over the stream [ACK19] and that there is a randomized semi-streaming algorithm for MIS in O(log log n)
passes [ACG+15] (see also [Kon18]). But, what is the best number of passes possible for this problem? Can
we prove a lower bound stronger than single-pass algorithms? What about an upper bound of o(log log n)
passes? There are several other related questions in this domain that can be tackled during the project.
References:
[ACG+15] Kook Jin Ahn, Graham Cormode, Sudipto Guha, Andrew McGregor, and Anthony Wirth. Correlation clustering in data streams. In Francis R. Bach and David M. Blei, editors, Proceedings
of the 32nd International Conference on Machine Learning, ICML 2015, Lille, France, 6-11 July
2015, volume 37 of JMLR Workshop and Conference Proceedings, pages 2237-2246. JMLR.org,
2015.
[ACK19] Sepehr Assadi, Yu Chen, and Sanjeev Khanna. Sublinear algorithms for (Δ + 1) vertex coloring.
In Timothy M. Chan, editor, Proceedings of the Thirtieth Annual ACM-SIAM Symposium on
Discrete Algorithms, SODA 2019, San Diego, California, USA, January 6-9, 2019, pages 767-
786. SIAM, 2019.
[Kon18] Christian Konrad. MIS in the congested clique model in o(log log Δ) rounds. CoRR,
abs/1802.07647, 2018.
Locality Sensitive Hashing in Hamming Metric
Project #: DC2022-06
Mentor: Karthik Srikanta, Computer Science
Abstract: Given a set of n points in a metric space, find a pair of points with the smallest distance between them. This computational problem is referred to as the closest pair problem [1] and is a fundamental problem in computational geometry with applications to various areas of computer science such as computer vision and machine learning. In high dimensions, it is known that no algorithm can exactly solve the closest pair problem much faster than naively computing all pairwise distances [2]. However, if one settles for approximate solutions, then the celebrated technique of Locality Sensitive Hashing [3] (LSH) provides a fast way to compute approximate solutions. The goal of this project is to first survey the existing literature on LSH [4], and then focus on exploring the connections between LSH in the Hamming metric and Coding theory [5]. At a technical level, the project would involve designing and analyzing various algebraic and combinatorial objects to better understand a geometric computational problem.
[1] https://en.wikipedia.org/wiki/Closest_pair_of_points_problem
[2] https://link.springer.com/article/10.1007/s00493-019-4113-1
[3] https://en.wikipedia.org/wiki/Locality-sensitive_hashing
[4] https://www.mit.edu/~andoni/LSH/
[5] https://mathworld.wolfram.com/CodingTheory.html
The wisdom of the market
Project #: DC2022-07
Mentor: David Pennock, DIMACS
Abstract: A prediction market share pays $1 if a future event happens, like a wealth tax is adopted by 2022, and $0 if not. The market price can be thought of as a consensus estimate of the probability of the event. If all traders optimize according to the so-called Kelly criteria, then the market price evolves like a machine learning expert algorithm, guaranteed to be not much worse than the most accurate trader. In this project, we will explore new variations on this theme. What happens if traders optimize in a different way? What if traders themselves learn over time how accurate they are compared to the market price? We will investigate the problem using simulation and theory.
Characterizing revenue non-monotonicity for two identical, independent items
Project #: DC2022-08
Mentor: Ariel Schvartzman, DIMACS
Abstract: Suppose a seller wants to sell an apple to one of two buyers, Alice and Bob, who draw their value for the apple from some known distribution D_A, D_B. Suppose that Alice's distribution stochastically dominates Bob's. Formally, for all x the probability that Alice values the apple at x or higher is greater than the probability that Bob values the apple at x or higher. If the seller is trying to maximize their revenue, they would always prefer to sell the apple to Alice rather than Bob. Surprisingly, if there are two, identical apples for sale, there exist cases where the seller would get more revenue from selling to Bob than to Alice. This is an example of revenue non-monotonicity, a counterintuitive and strange property. The purpose of this project is to characterize when revenue monotonicity holds. Intuition suggests that if one distribution "greatly" stochastically dominates another, then revenue monotonicity should hold.
Preference will be given to candidates with some exposure to mechanism design or algorithmic game theory, but all candidates who are interested in learning will be considered.
The DLC Problem: how to price additional content?
Project #: DC2022-09
Mentor: Ariel Schvartzman, DIMACS
Abstract: Many digital games have "downloadable content" (DLC), which is additional content a user pays for to enhance their gaming experience (e.g., more levels, more characters, etc). Suppose we are selling a game to a buyer who draws their value for the game v from some known distribution D. The game also has one DLC that requires the base game to be purchased - there is no value in purchasing the DLC alone. If the buyer purchases the game, they can learn their value v' drawn from some other D' for the game and DLC (where v' >= v), and then decide whether or not to buy the DLC. What is the optimal price for the game and the DLC?
Exploring the tradeoffs between compression and performance in deep neural networks
Project #: DC2022-10
Mentor: Waheed Bajwa, Electrical and Computer Engineering
Abstract: The practice of artificial intelligence / machine learning has advanced tremendously
in the last decade, and much of it has to do with advances in deep neural networks (DNNs). But some of
the best results in DNNs have been obtained for the case when the neural network has tens of millions of
parameters. Storage of such networks, as well as inference using them, becomes challenging in the case of
resource-limited portable devices, such as smartphones, sensing devices, etc. Compression of DNN weights
has been proposed as a solution to this challenge, and several different approaches to compression have been
put forth in this regard. Such compression of DNNs however comes at the cost of reduction in inference
performance, with different approaches giving rise to different tradeoffs between compression and performance.
In this project, we will explore the tradeoffs between compression and performance for different methods that
have been proposed in the literature, and we will attempt to propose an alternative strategy for compression
based on tensor factorization that might outperform the existing methods.
Prerequisites: Students interested in this project are expected to have a good command of (numerical)
linear algebra, calculus, and Python programming, and some familiarity with deep neural networks as well as
one of the deep learning frameworks such as PyTorch and TensorFlow. Prior experience with cloud computing
and/or cluster computing is useful, but is not a prerequisite.
Identifying Motifs in Brain Connectome Data
Project #: DC2022-11
Mentor: Jie Gao, Computer Science
Abstract: Brain connectome studies neural connections in the brain, modeled by a graph with vertices representing groups of neurons and edges representing the correlation of the neuron activities. In this project we will study the properties of such brain network data using graph theory and complex network analysis. This project focuses on identifying motifs, small network building blocks that are prominent in the network. On brain networks, motifs are characterized as structural motifs, which quantify anatomical building blocks, and functional motifs, which focus on elementary processing modes in a network. Most of the current work on motif discovery focuses on motifs of tiny sizes (with a constant number of vertices). For example, it was discovered that open bidirectional wedges are one of the motifs that are key to structural hubs in the brain. In this project we explore efficient algorithms to identify motifs of larger sizes. The problem is connected to topics in data mining especially frequent pattern mining.
Graph Cities
Project #: DC2022-12
Mentor: James Abello, Computer Science
Abstract: "Graph Cities" are 3D representations of maximal edge graph partitions. Each connected equivalence class corresponds to a "building" that is formed by stacking graph "Edge Fragments". The number of such graph edge fragments determines the height of the building. The overall number of buildings is the number of equivalence classes in the edge partition.
In this project, REU participants will build "Graph Cities" from data collections containing at least a billion related entity pairs. Each created "City" will come equipped with a "Story" plus an accessible catalogue of its most prominent "locations", "entities", "landmarks", and "Subgraph Motifs". Each discovered motif will be judged according to its "provenance" and a profile that may include measures of "density", "diversity" , "surprise", and "interestingness".

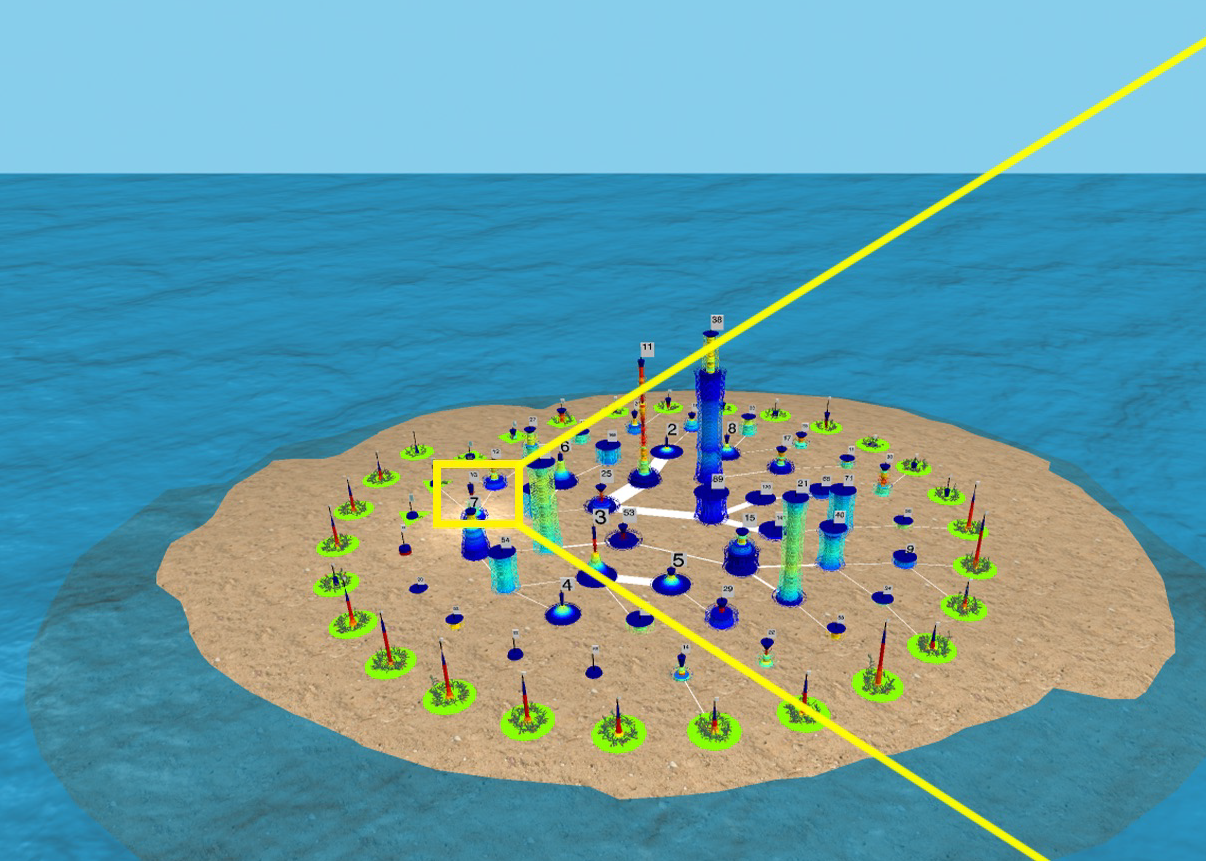
Please read more details in this pdf file.
Pre-Requisites:
Programming Languages: JavaScript and two languages from {Python, Java, C/C++}.
Algorithms/Optimization: A class on Algorithms and a second class in Optimization or Graph Theory.
Reading List: Become familiar with at least 7 papers from the list in the detailed project description before the beginning of the REU.
Projects in Pure Math
Project #: DC2022-13
Mentor: Faculty of the Math Department, Mathematics
Abstract: The Math REU Coordinator is Prof. Kristen Hendricks. Several projects will be run in 2021 by members of the pure math faculty. Past topics have included Schubert Calculus (Buch), Lie algebras (Lepowsky), mathematical Yang-Mills theory (Woodward), etc. Applicants interested in a project in pure mathematics should list this project in their application and indicate their specific Math interests; further details on the projects will be worked out in the Spring.
Mathematical Physics in One Space Dimension
Project #: DC2022-14
Mentor: Shadi Tahvildar-Zadeh, Mathematics
Abstract: Imagine the universe consisted only of beads of different size and color on a single string, with some rules about how they would interact, combine, separate from, or bounce off one another. How would familiar notions of classical physics such as gravity or electromagnetism look like in such a universe? What about quantum phenomena? How far can one go on this quest? Is it feasible to look for a one-dimensional "theory of everything"?
The goals of this REU project are to
- introduce students to the mathematical tools they need in order to understand these questions,
- help them use those tools to find satisfactory answers to some of the questions
- give them the vocabulary they need in order to ask many more such profound questions, not just about this cartoon world, but also about the actual world we live in.
The emphasis will be on mathematical rigor and exact analysis. Previous knowledge of physics is welcome but not required. Mathematical knowledge at the level of Calculus 3 and Linear Algebra is required, as is familiarity with at least one computational software such as Matlab, Maple, or Mathematica.
Projects in Arithmetic, Geometry, and Dynamics
Project #: DC2022-15
Mentor: Alex Kontorovich, Mathematics
Abstract: A number of problems will be proposed at the interface of the topics in the title, and students will work in groups, together with graduate students and postdocs, on projects ranging from the purely theoretical to the numerical/experimental. If there is interest, some of the projects can involve formalized mathematics in the Lean interactive theorem prover.
Genome folding and function: from DNA base pairs to nucleosome arrays and chromosomes
Project #: DC2022-16
Mentor: Wilma Olson, Chemistry and Chemical Biology
Abstract: Despite the astonishing amount of information now known about the sequential makeup and spatial organization of many genomes, there is much to learn about how the vast numbers of DNA base pairs in these systems contribute to their three-dimensional architectures and workings. The chemical structure of DNA contains information that dictates the observed spatial arrangements of base pairs within the double helix and the susceptibilities of different base sequences to interactions with proteins and other molecules. Our group has been developing software to analyze the spatial and energetic codes within known DNA structures and using these data in computational studies of larger nucleic acid systems (1). By representing the DNA bases as sets of geometric objects, we can capture the natural deformability of DNA as well as the structural details of ligand-bound interactions (2). There are now sufficient data to examine the influence of sequence context, i.e., the effects of immediate neighbors, on the apparent motions of the bases and to develop simple functions that capture this information. The observed behavior can be incorporated in computational treatments to improve our understanding of macromolecular systems in which DNA sequence and protein binding play important roles. For example, DNA elements that regulate gene expression often lie far apart along genomic sequences but come close together during genetic processing. The intervening residues form loops, mediated by proteins, which bind at the sequentially distant sites. We have developed methods that take account of both DNA and protein in simulations of loop formation and successfully captured experimental observations (3,4). Our recent studies of long-range communication between regulatory elements on short nucleosome-decorated DNA (5,6) provide a basis for linking the 'local' arrangements of nucleosomes in these systems to higher-order macromolecular structures, such as the looped architectures detected within chromosomes. We are developing new algorithms to characterize the spatial arrangements of nucleosomes and incorporating the collective information in nucleosome-level depictions of chromosomal DNA (7,8). The build-up of structural components in our treatment of DNA and chromatin offers new insight into the stepwise processes that underlie genome organization and processing.
References:
1. Olson, W.K. 2020. "Insights into DNA and chromatin from realistic treatment of the double helix," in Paul Flory's 'Statistical Mechanics of Chain Molecules' Today, A.C.S. Books, Tonelli, A.E. and Patterson, G.D., Eds., American Chemical Society, Washington, D.C., Chapter 9, pp. 143-159.
2. Tolstorukov, M.Y., A.V. Colasanti, D. McCandlish, W.K. Olson and V.B. Zhurkin. 2007. A novel roll-and-slide mechanism of DNA folding in chromatin: implications for nucleosome positioning. J. Mol. Biol. 371:725-738
3. Wei, J., L. Czapla, M.A. Grosner, D. Swigon and W.K. Olson. 2014. DNA topology confers sequence specificity to nonspecific architectural proteins. Proc. Natl. Acad. Sci. USA 111:16742-16747.
4. Clauvelin, N., W.K. Olson. 2021. Synergy between protein positioning and DNA elasticity: energy minimization of protein-decorated DNA minicircles. J. Phys. Chem. B 125:2277-2287
5. Clauvelin, N., P. Lo, O.I. Kulaeva, E.V. Nizovtseva, J. Dias, J. Zola, M. Parashar, V. Studitsky and W.K. Olson. 2015. Nucleosome positioning and composition modulate in silico chromatin flexibility. J. Phys.: Condens. Matter 27:064112.
6. Nizovtseva, E.V., Todolli, S., Olson, W.K., and Studitsky, V.M. 2017. Towards quantitative analysis of gene regulation by enhancers. Epigenomics 9:1219-1231.
7. Todolli, S., P.J. Perez, N. Clauvelin and W.K. Olson. 2017. Contributions of sequence to the higher-order structures of DNA. Biophys J. 112:416-426.
8. Todolli, S., R.T. Young, A.S. Watkins, A. Bu Sha, J. Yager, and W.K. Olson. 2021. Surprising twists in nucleosomal DNA with implication for higher-order folding. J. Mol. Biol. 167121.
Deep genomic analysis of tumor specimens
Project #: DC2022-17
Mentor: Hossein Khiabanian, Rutgers Cancer Institute of New Jersey
Abstract: Understanding complexity, dynamics, and stochastic patterns in genomic data - concepts native to physics and mathematics - is critical for elucidating how disease states originate and evolve. The main focus of this project is to use statistical, information theoretic approaches to dissect the cellular and molecular heterogeneity that enables cancer cells to evolve. We use high-throughput DNA sequencing methods, and computationally integrate genetic and clinical data from large cohorts of cancer patients being treated under various precision medicine programs, with the aim to identify markers of Darwinian selection using longitudinal data. Our ultimate goal is to develop novel statistical platforms for fast translation of genomic data into clinical practice.
Proficiency in programming and statistical analysis are essential; knowledge of genomics and biology is not required but highly valued.
Genomic data-guided mathematical modeling of cancer
Project #: DC2022-18
Mentor: Subhajyoti De, Rutgers Cancer Institute of New Jersey
Abstract: Cancer is the second leading cause of death in adults, claims the lives of more than half a million Americans every year. Tumor starts from a single rogue cell in the body, which becomes defective, and the clones of that initial cell start to grow (or die out), and acquire new mutations depending on certain parameters stochastically; and by the time of detection the tumor has ~10^9 cells.During treatment, the patients initially responds and the tumor shrinks,but remaining cells inevitably develop mutations that give them drug resistance, and the tumor starts to grow again until the patient dies. It is becoming apparent that computational algorithms and mathematical frameworks can identify subtle patterns in patient profiles, which can help with early detection and personalized treatment, improving their outcome. For instance, we are developing mathematical frameworks to model tumor development and emergence of resistance against cancer drugs, using Galton Watson branching process - an area of stochastic processes,which also has applications in diverse areas. We are combining mathematical models with clinical data from cancer patients to ask some fundamental questions: (i) how long does it take a tumor to grow, and can we detect cancer early? (ii) can we identify emergence of resistance very early and accordingly change the treatment strategy? The project will aim to develop mathematical frameworks to model tumor growth using branching process.
Proficiency in computer programming (Java, C++, or python),familiarity with probability theory, concepts of stochastic processes,and optimization techniques are required. Knowledge in Biology is not required.
Data-driven precision medicine approaches to cancer
Project #: DC2022-19
Mentor: Subhajyoti De, Rutgers Cancer Institute of New Jersey
Abstract: One in four is expected to develop cancer in their lifetime. No two patients are alike, and we need better strategies to detect cancer early,find right treatment for the patients, and monitor their outcome using a personalized medicine approach. Data science approaches using state-of-the-art computational algorithms and statistical frameworks can identify subtle patterns sifting through large amount of information in patient profiles, which can help with early detection and personalized treatment, improving their outcome. Within the scope of the Precision Medicine Initiative at the Rutgers Cancer Institute, for each patient we have troves of data on genetic mutations, and clinical and pathological reports. We are developing and implementing data science techniques to ask some fundamental questions: (i) can we distinguish aggressive tumor and treat patients accordingly? (ii) can we identify emergence of resistance very early and accordingly change the treatment strategy? The project will aim to develop data science frameworks to perform integrative analysis of cancer genomics and clinical data.
Proficiency in computer programming (Java, C++, or python), statistical analysis software (R or SAS), familiarity with concepts such as linear models, model selection, support vector machines are preferred. Knowledge in Biology is not required.
The Curse of Many: The Combinatorial Challenges of Many Robot Arms Manipulating Many Objects
Project #: DC2022-20
Mentor: Kostas Bekris, Computer Science
Abstract: Robotic arms are increasingly being deployed in logistics or the service industry, where they are often tasked to manipulate and rearrange multiple objects. Planning a robot's motion so that it avoids undesirable collisions, i.e., the robot motion planning problem, is already a computationally hard challenge. The presence of multiple objects or multiple arms introduces additional combinatorial challenges that need to be addressed (task planning), such as identifying the right order of objects to move as well as the proper coordination of multiple arms operating in the same workspace. Current solutions tend to face scaling challenges as the number of objects and arms increases. This REU project will build on state-of-the-art task and motion planning algorithms in this space. It will explore setups where it is possible to identify methods that can deal with the combinatorial explosion as the number of objects and arms increases. For instance, we have shown in existing work that dual-arm tabletop rearrangement of multiple objects can be decomposed into sub-problems that possess efficient polynomial-time approximation algorithms. The key idea is that the optimal solution requires an optimal assignment of objects to arms and an optimal sequence of such combinations of arm-object pairs to be moved. The first subproblem maps to weighted edge-matching on a graph and the sequencing subproblem maps to a traveling salesperson problem. Both these subproblems lead to very efficient solutions that incur bounded suboptimality yet demonstrate substantial gains in computation time and scalability. It shows how using insights from algorithmic research provides useful tools for robotics. Depending on the student's prior experience and interests, this REU project can involve: (i) exclusively algorithmic design and analysis, and/or (ii) simulating such problems (e.g., by using popular robotic simulation tools, such as Gazebo or pyBullet and available motion planning software) and developing/testing algorithmic solutions. Depending on progress and through collaboration with PhD students, the results can be transferred on a real system and result in a publication. We are also open to project ideas proposed by REU students, which relates to applications of Foundational Computer Science and Mathematics in Robotics.
Task Planning for Object Manipulation: A Structural and Algorithmic Study
Project #: DC2022-21
Mentor: Jingjin Yu, Computer Science
Abstract: Effective manipulation of many objects, a task and motion planning challenge that remains difficult for machines to master, is essential in fulfilling the true potential of autonomous robots. One key mathematical/algorithmic problem in the domain is task planning for manipulation. For example, to tidy up a messy desk with many objects, assuming that a robot can work with one object at a time, the sequence with which to handle the objects sequentially has a direct impact on efficiency. Computing a high-quality sequence, however, is a computationally intractable problem in general. Depending on the particular task at hand, many interesting models arise with rich and intriguing structures [1][2]. While we have made significant progress in the past few years, we really have only touched the tip of the iceberg in tackling task planning for manipulation. An REU student, working under this topic, will help unveil the structures of manipulation problems and use the gained insight to develop state-of-the-art algorithms for the same.
[1] https://arc-l.github.io/pages/rss-21.html
[2] https://arc-l.github.io/pages/kai-rss-21.html
Statistical inference and automatic differentiation of iterative algorithms
Project #: DC2022-22
Mentor: Pierre Bellec, Statistics
Abstract: The goal of the project is to explore possible applications of automatic differentiation to help with the construction of confidence intervals and other statistical goals. Automatic differentiation is a powerful numerical tool to compute gradients functions, with no computational overhead compared to evaluating the function itself. It has found numerous applications in recent years, for instance it is the basis of modern deep learning implementations. Statistical inference in high dimensions aim to construct confidence intervals for unknown parameters, e.g., to quantify with high confidence the effect of a given human gene for a medical outcome of interest. Recent advances allow to construct such confidence intervals using the gradients of certain ideal functions of the observed data; these ideal functions are typically approximated by iterative algorithms. One possible research direction is to explore, numerically, the behavior of automatic differentiation when applied to these iterative algorithms: how do the computed gradients behave through the iterations, how well do they approximate the gradients of the ideal functions of interest, do confidence intervals built using these gradients yield valid statistical inference.
Data Privacy and Open Science
Project #: DC2022-23
Mentor: Ruobin Gong, Statistics
Abstract: The digital world we live in produces an explosive amount of personal data, from demographic
surveys to biomedical studies, and to user information from massive online platforms such
as Facebook and Netflix. If these data are translated into open-source databases accessible
for scientific research, they may become invaluable resources in fostering public knowledge
and improving research reproducibility. The challenge, however, is to do so without posing
an undue risk of exposing the confidential information of respondents, patients and clients.
This project explores the potential of modern privacy methods in the various data-driven
disciplines, including (but not limited to) the biomedical sciences, the behavioral sciences, as
well as the demographic, social, and political sciences. Recent advances in the data privacy
literature, notably differential privacy, presents a promising path towards facilitating open
science with open data, while ensuring the reliable protection of the privacy of individual data
contributors. The project asks the following questions: what is the current state and mindset
of data privacy protection in the subject matter discipline? In what ways can cutting-edge
privacy methods help promote data sharing, transparency, and informed science? How can
existing privacy methods apply to some of the concrete use cases?
This project will be suitable for a student in a subject matter discipline (such as those listed
above) with a demonstrated interest in the quantitative approach to the scientific discourse.
The ideal candidate is a student who has taken, and excelled in, courses in both a subject
matter science and in computer science and/or statistics, with experience in writing data
analysis programs in R or Python.
Applicant Responsibilities:
The student will be responsible for identifying an interested area of application, conducting
the literature review, connecting and extending suitable privacy methodologies to the application, performing data analysis as necessary, and summarizing the research findings into a
rigorous academic report.
Searching faster for better programs
Project #: DC2022-24
Mentor: Srinivas Narayana, Computer Science
Abstract: Compilers like gcc turn programs in a higher-level language (like C++) into efficient assembly code, implementing many optimizations to the code in the process. A special class of compilers, called superoptimizing compilers, search for the optimally-performing version of a given program. The caveat is that this search is only tractable for small programs, say, about a hundred assembly instructions long, since the space of possible programs explodes quickly with program size. This summer project will explore new program search algorithms geared to find better-performing programs faster than the state of the art, in the context of a domain-specific superoptimizing compiler for networking[1]. The student will be provided a background in formal methods to model the semantic behavior of computer programs, explore a variety of algorithms for program search, and work with system software that extends operating system kernels. This project requires both algorithmic thinking and prototyping efforts. Familiarity with Linux and programming is required. There is an option to continue working on the project beyond the summer. Contact: sn624@cs.rutgers.edu
[1] https://www.cs.rutgers.edu/~sn624/papers/k2-sigcomm21.pdf
Projects on Data Analysis
Project #: DC2022-25
Mentor: Christie Nelson, Masters of Business and Science in Analytics and CCICADA
Abstract: The following projects will be supervised by Dr. Nelson: 1. Modeling Human Trafficking, 2. Text Analysis of Prosecuted Federal Crime Data, 3. Walk Through Metal Detector Detection Analysis.
For details, please see this pdf file.
Simplifying explicit equations of fake projective planes
Project #: DC2022-26
Mentor: Lev Borisov, Mathematics
Abstract:
Generalizing the Fortuin-Kasteleyen-Ginibre inequality
Project #: DC2022-27
Mentor: Siddhartha Sahi, Mathematics
Abstract:
Cryptography and computational complexity
Project #: DC2022-28
Mentor: Marshall Ball, Department of Computer Science, Courant Institute of Mathematical Sciences, NYU
Abstract:
 Return to REU Home Page
Return to REU Home PageDIMACS Home Page
DIMACS Contact Information
Page last modified on December 13, 2021.