
DIMACS REU 2016

| Name | Thomas Murrills |
|---|---|
| School | Rutgers University |
| thomasmurrills | gmail | |
| Project | Interpolation between Perseus and Diamorse paradigms of persistent homology computation on grayscale images |
Project Information
Mentors
Context
Persistent homology computations on grayscale images rely on representing pixels as cell complexes. How exactly do we do this?
There are two topologically inequivalent methods: we can consider pixels to be points, connected by edges and a face at pixel borders and corners, respectively; or we can consider them to be squares, complete with four edges and four vertices, which overlap on pixel borders and corners. (These two paradigms will be here known as the Diamorse and Perseus paradigms, respectively, after algorithms that employ them.)
The choice of which paradigm to employ in practice is arbitrary unless the properties of the image source considered interesting to the application at hand have some relevance to our interpretation. Moreover, these two approaches do not in general yield the same persistent homologies, as is often assumed in the literature.
For example, consider a two-by-two image with grayscale values as below.

For any threshold value between 0 and 255, here’s what the cell complexes (on which the homology is computed) of the two different paradigms look like:
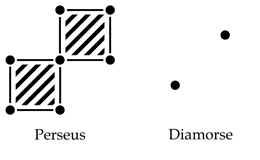
The Perseus paradigm yields one connected component, whereas the Diamorse paradigm yields two. However, the choice between Perseus and Diamorse is arbitrary. How can we understand their differences and, to some extent, reconcile them?
Research
Weekly Log
These will necessarily be somewhat cryptic until publication.Week 1
Recognized the need for a criterion that captures the relevant homology distinction. Constructed fundamental regions with respect to pixels. Found a description of P/D in terms of these fundamental regions. Met with Rachel, and was pointed in the direction of constructing a homotopy equivalence which would imply homology equivalence. Attempted to capture homotopy equivalence in terms of fundamental regions and 'connections' among them, but also started to move in the direction of simply reasoning about CW complexes, at Rachel's recommendation.
Created the introductory presentation!
Week 2
Still trying, in part, to write down the necessary criterion. Started to think about a sense of 'free closure' of subsets of CW complexes, but also thinking more about connection (of fundamental regions) and homotopy, since isomorphism of the fundamental groups of CW complexes implies homotopy equivalence. Attempting to define 'direct connection'. In any case, realized that I can live with a one-way implication (some rather strict relation between CW complexes implies homotopy equivalence) and show that the algorithm produces an image that satisfies that.
On the side of proving the validity of the algorithm, constructed 'configurations' and 'environments', among other notions, to talk about the conditions the c-value must satisfy and prove that it does, indeed, satisfy these.
From these constructions, figured out the c-value determination algorithm precisely. Wrote the algorithm in MATLAB! Still need to include better user-specified file flow.
Week 3
Defined free closure on subsets of CW complexes! A long and careful definition, yet nice. Arrived at a conjecture about free closures which I suspect is true with greater generality than necessary for this research! Thinking about how to relate it to the partial ordering on the cell complex explicitly.
Used the configuration-related constructions to more fully show the validity of the algorithm, and communicated such to Rachel.
Week 4
Breakthrough! Found a simple explicit deformation retract, and then realized this deformation retract in terms of the barycentric subdivision of the complex. Found a realization of the barycentric subdivision in terms of subdiagrams of the Hasse diagrams isomorphic to the Hasse diagram of the power set on n elements. [Later, I found this was only happenstance due to the simplicial nature of the neighborhoods of cells in cubes.]
Phrased this categorically in terms of the category of (2-)factorizations in the category of injective functions on finite sets (monfset2 and monfset) and how the relationship between monfset2 and monfset may be extended along the power set functor from monfset to monHposet, where arrows in monHposet are those of monposet but preserve factorizability (and thus the Hasse diagrams). (I expected a Kan extension.) The barycentric subdivision of a complex would then be a certain comma category from this extended functor to that complex realized as an object in monHposet.
Rachel introduced me (via a professor) to a subdivision of categories known as Segal subdivision. It agreed with my Hasse subdiagram subdivision as far as I tested it. I was not sure how to relate this to the Hasse subdiagrams, except that it likely involved factorizations of the arrow from the initial object to the terminal object in the power set poset of a set of n elements.
Created relevant bitmap test images to feed into the algorithm from which to generate persistence diagrams to explore the effect of the algorithm explicitly.
Sketched an outline of the proof as a whole.
Week 5
Spent some time exploring the relationship between the Hasse subdivision and Segal subdivision. Discovered that the Hasse subdiagram version of barycentric subdivision does not work as intended—the Hasse subdivision of an octahedron, realized as a cell complex, would have no 3-cells! Formalized why Segal subdivision captured barycentric subdivision well, and proceeded with Segal subdivision.
Resources
Background – Intuition
Persistent homology captures the way topological features of a space change as we ‘grow’ the space over the course of some parameter. Consider a grayscale image, and take our ‘spaces’ to be, essentially, the set of pixels with grayscale value below some particular arbitrary grayscale value. This space has some homology. To understand the image as a whole, we vary that arbitrary grayscale threshold value from the minimum to the maximum. For each grayscale value in this range we obtain a ‘sublevel set’ of pixels, which grows as we increase the threshold value, allowing more and more pixels in.
Clearly, the homology of these sublevel sets will in general be different over the course of this parameter—for example, if we have an image with two separated dark spots (which have low grayscale values), then as the threshold value increases, we will have, in sequence, no connected components, one connected component (when the darkest pixel of the darker spot ‘pops in’), two (when the darkest pixel of the second spot pops in), and one (when the pixels in between the spots bridge the gap).
How exactly the homology changes in this way is captured in the persistent homology: homological features, i.e. connected components or holes, are ‘born’ and ‘die’ over the course of the threshold value increasing. These ‘births’ and ‘deaths’ can be put together in a ‘persistence diagram’, which is a 2D scatterplot with threshold values along each axis. For each homological feature, the (birth, death) threshold values of that feature form the (x, y) coordinates of a point which is plotted on the diagram. These lists of (birth, death) pairs are the data on which statistics and machine learning can be performed.
Further Background, Presentation, and External Resources
Coming soon!Special Thanks
- Lazaros Gallos : REU director
- Érik de Amorim : REU graduate assistant