
Joy Hamlin's REU 2020 Web Page

General Information
| Name: | Joy Hamlin |
|---|---|
| Email: | joy.hamlin (at) rutgers.edu |
| Office: | N/A |
| School: | Stony Brook University |
| Project: | Research Into Smale's 7th Problem |
Project Description
Consider some number of particles on a sphere with an energy function based only on their relative positions. Smale's 7th Problem asks for a configuration that minimizes the total energy, or at least comes sufficiently close. As the number of particles increases, there are exponentially many configurations that are local minimizers of energy, which makes both an exhaustive search and random sampling infeasible. We investigate cases with a small number of particles, looking for a complete description of the energy of any configuration.
Weekly Progress
Week 1
I looked at several papers on Smale's 7th Problem, to get a sense of what I could be doing. I chose the paper listed (1) below, a complete exploration of the case with three particles restricted to a circle. The next step is to explore the four particle problem, in its full generality on a sphere. To do that, we start by investigating the circle again. After getting a sense of what my project was, I created a presentation to explain it to the rest of the REU. In addition, I learned how to create a website, and set up this page!
Week 2
I began a survey of the degernate four particle arrangements, where at least two of them occupy the same point. I started with the cases where at most two distinct points are occupied, producing a graph of compactified average pair energy aginst the s parameter:
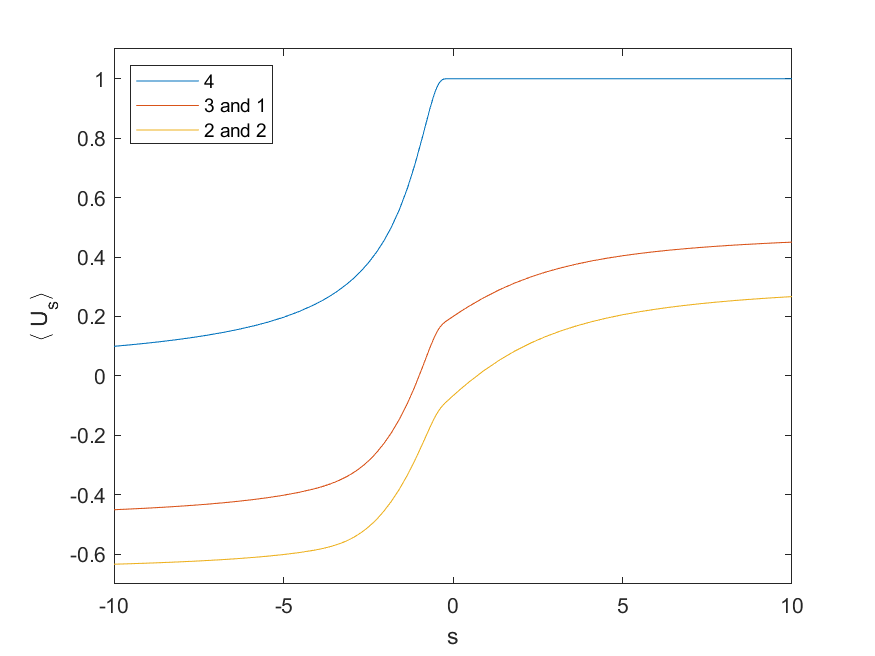
I also began an analysis of the case where the four points occupy three distinct locations, computing the average compactified pair energy for all possible isoceles triangle formations.
Week 3
I partially prooved that an arrangement with four particles taking up three distinct points must in fact be an isoceles triangle on a great circle, as well as a proof that for s=-2, a nondegenerate configuration of any number of points is an equilibrium iff its center of mass is at the origin. From there, I found some isoceles equilibria that had never been noticed before, though I have not yet proven this result. Finally for this week, I began an investigation of the case with four particles on a great circle, creating graphs and investiagtions of the rectangular and kite configurations.
Week 4
I finished up the investigation of the rectangular and kite configurations that I started last week, managing to prove that there are no nonsquare rectangular equilibria for s≠-2 and finding unexpected kite equilibria for s values below roughly -8.8. I moved on to trapezoidal cases, which have more degrees of freedom and thus require three dimensional graphs to be able to see their shape. As such they were harder to analyze, but it seems as though there are no nondegenerate trapezoidal equilibria (counting a square as a degenerate trapezoid). I tried to prove more of my results from the past few weeks, but the rectanglular configuration proof was the only one that was particularly tractable for me.
Week 5
This week, I have moved on to the truly three dimensional configurations of particles, starting with tetrahedra that have equilateral bases. I showed that such a base must always be below the xy plane, assuming the apex is at (0,0,1), and found one family of equilibria for s≥-2 and two families for s<-2. After that I moved to tetrahedra with four congruent isoceles faces, and then ones with two pairs of congruent iscoceles faces, finding one new family of equilibria in the former case and none in the latter. The last set of 3D configurations to consider is ones with two congruent scalene triangle faces sharing an edge, which is more complicated than the other cases.
Week 6
I started by looking at the configuration mentioned above in Cartesian coordinates, trying to prove that any equilibrium has to degenerate into a more symmetric case. That route didn't provide anything of use, so I switched to spherical coordinates, fixing two of the points in position and varying the positions of the third and fourth, but having those ones locked in place relative to each other. This reduced it from a three parameter problem to a one parameter problem, but the equilibria I found there don't have to correspond to any true equilibria once the other points are free to move again. We gave up on that problem and moved back to the case where two particles share a point, since there are some scalene equilibria to observe there.
Week 7
We realized that the reason we couldn't prove that all equilibria on a great circle are reflection symmetric about a diameter is because it isn't actually true, there are scalene equilibria for s<-2. It starts as a degenerate antipodal arrangment at s=-2 and becomes a proper scalene triangle from there as s decreases. After that, I went back to the tetrahedron with two pairs of congruent isosceles faces, finding that the regular tetrahedron goes from a saddle point to a maximum around s=-6. This suggests the existence of sattelite equilibria, and after more investigation those were in fact discovered.
Week 8
This week was focused on properly writing up proofs and creating my final presentation. No new results were found, but the ones from the previous weeks were put together in a clearer manner.
Week 9
This week was very similar to last week. I finalized and presented my final presentation, and wrote up my reflections about the program.
References
- Hilbert's "monkey saddle" and other curiosities in the equilibrium problem of three point particles on a circle for repulsive power law forces, Michael K.-H. Kiessling and Renna Yi - ArXiv.
Additional Information
- My Mentor
- Other Participants In This REU
Work supported by the Rutgers Department of Mathematics and NSF grant DMS-2019396.