Week 5. "Starrifying" Graphs

I proposed and tested a number of conjectures for algorithms to iteratively change graphs into stars while simutaneously reducing the weight of the mapped Steiner tree in every step.

For several weeks, we thought that a naive algorithm of removing an edge and adding a new one to a max degree vertex would work. However, it turns out that there are many counterexamples. In order to check carefully, I wrote a lot of Sage code this week. I generated the optimal Steiner trees of every graph of size at most 10 and then tested numerous algorithms on the graphs.

I now have an algorithm that works at least on graphs of size at most 10 and which depends critically on my results from the previos weeks. I also proved a number of additional structural results this week and considered an odd one dimensional variant of the Steiner tree problem on trees in order to apply its properties in the harder $n$-dimensional Euclidean setting.

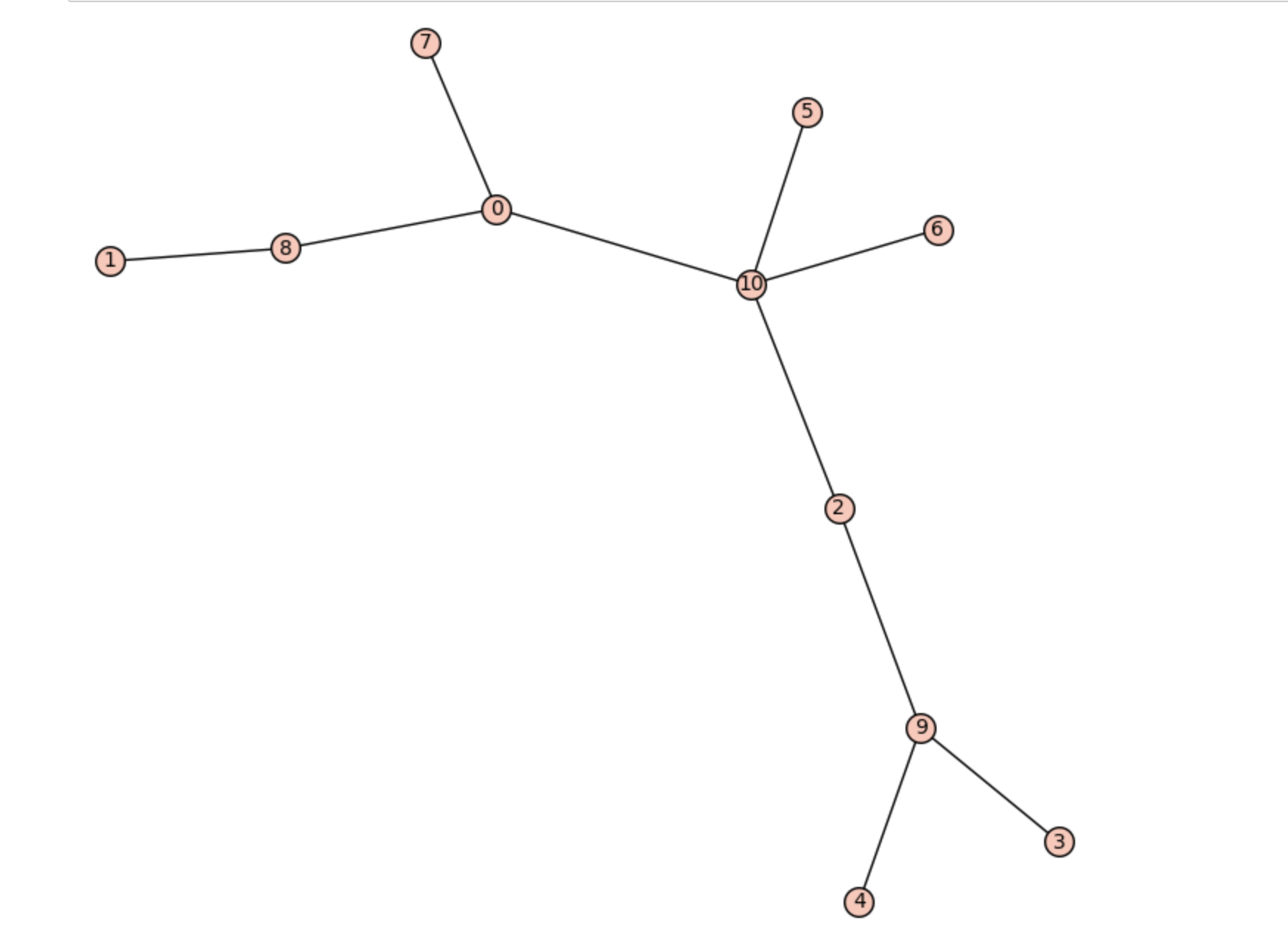
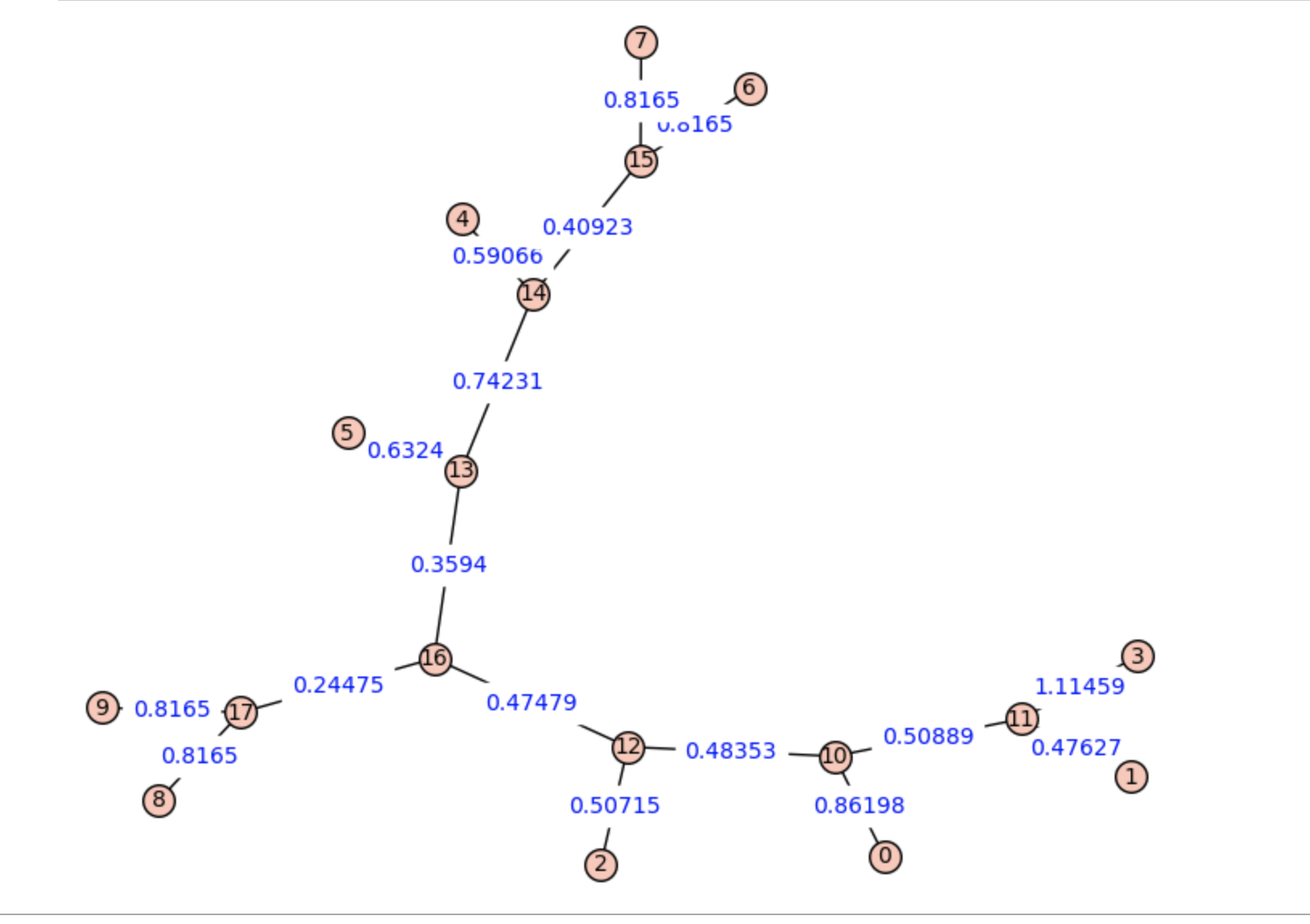
Below I include a picture of a graph and its optimal Steiner tree (of total weight $10.672$), generated by my Sage code.