Week 1. What is the Steiner tree problem?

Let $(U, d)$ be a finite subset of a large ambient metric space (say, $U \subseteq \mathbb{R}^2$ with the $\ell_2$-metric, for example).

The points $U$ induce a natural weighted complete graph $G = (V,E)$ with vertices $v \in U$ and edge weight of $(u_1, u_2)$ equal to $d(u_1, u_2)$. For notation, we refer to these points $U$ as "terminals.""

One can calculate the weight of a minimum spanning tree of $G$. In some cases, introducing additional points (called Steiner points) to the configuration can reduce the weight of a spanning tree of the points. The equilateral triangle is the classical example of a Steiner point reducing the weight of a spanning tree of the points. Without a Steiner point, the weight of an MST is $2$. With a Steiner point added in the middle, drawing the tree from the Steiner point to the terminals, the weight of the Steiner tree is $\sqrt{3}$.

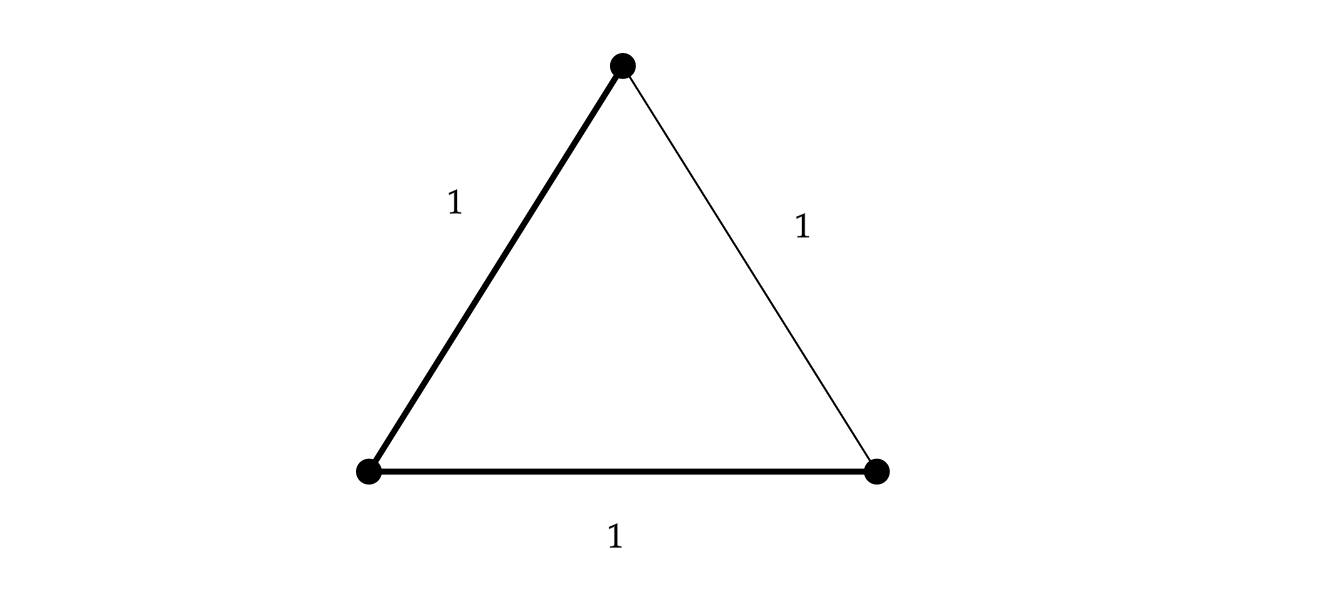
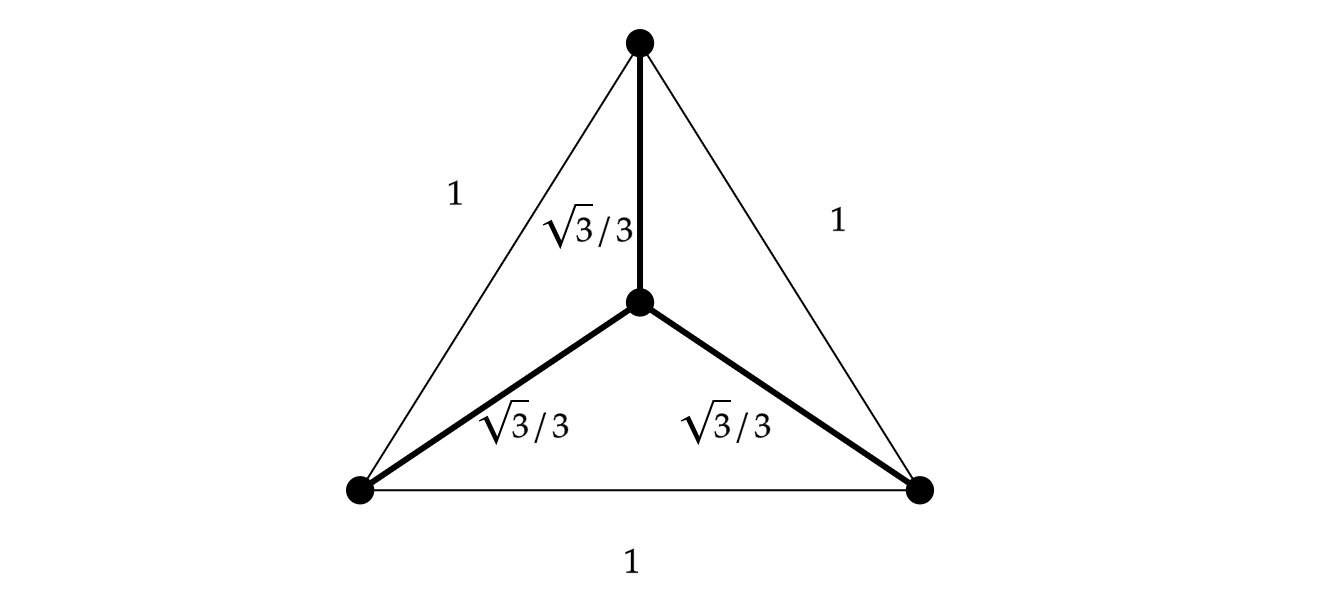
This turns out to be the optimal configuration, yielding a ratio (called the Steiner ratio) of $\sqrt{3}/2$. With the $\ell_2$-metric in two dimensions, this is the minimal known Steiner ratio. The best known lower bound on this quantity is $0.824$ from a landmark paper 1985 of Chung and Graham,

One of the problems for the summer is improving the bounds on the minimal Steiner ratio for a fixed metric in Euclidean space, especially in higher dimensions. In arbitrary dimensional Euclidean space, Du, Wu, Lu, and Xu showed a lower bound of $0.62$. In higher dimensions, the upper bound is actually better than a regular simplex (which yields a ratio of $0.669$) as shown by Du and Smith.

The other main problem for the summer is hardness of approximating optimal Steiner trees. More on that next week.