General Information

| Student: | Gabriel Eiseman |
|---|---|
| Office: | 446 |
| School: | Rutgers New Brunswick |
| E-mail: | hacatu5000@gmail.com |
| Project: | Sphere Packings and Discrete Mathematics |
Project Description
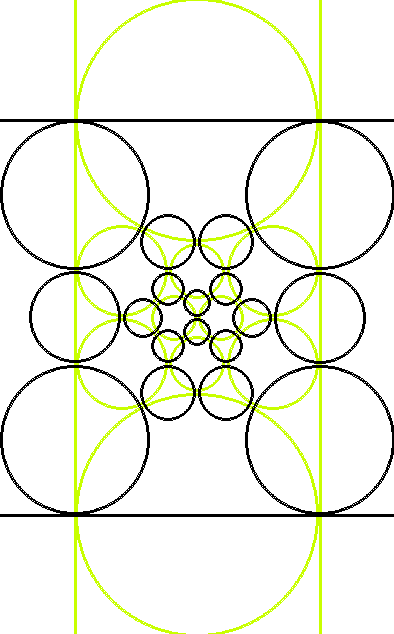
I am investigating patterns in sphere and circle packings, such as their generalizations to higher dimenstions, the appearance of dual polyhedral graphs in their Coxeter diagrams, and the minimum number of steps required to construct Apollonian circles.
The code for searching for six step constructions for Apollonian circles can be foud here
Weekly Log
- Week 1:
- I arrived at the progam and have been getting familiarized with the math behind sphere packings.
- Week 2:
-
This week I learned about polyhedral sphere packings and the Koebe-Andreev-Thurson theorem.
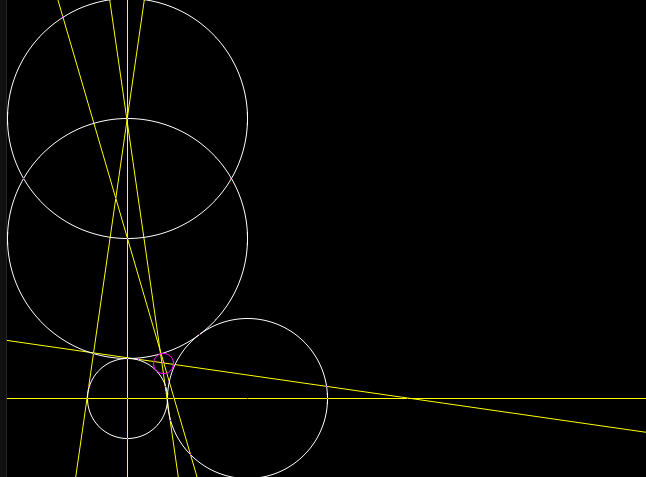
I made a program to compute circle packings from planar graphs and wrote and tested code to
work with compass and straightedge constructions. I can intersect lines and circles to
create points and connect points to create lines and circles. Since the thing we want to
construct is a circle tangent to three tangent circles, the sixth step of any six step construction
would have to be drawing the circle, which means after the fifth step we need a point of
intersection at the center of the goal circle and one on its edge, so after the fourth step
we need a line or circle through each of those two points. By the end of the week I was able to
successfully brute force circles where the triangle between their centers was equilateral or
isosceles, but I do not have a good way of verifying these approximate solutions.
- Week 3:
-
After spending a lot of time earlier in the week working on a way to exactly verify potential
constructions using a computer algebra system, it turned out to be far too slow given there are
half a million potential constructions (out of at most 18 quintillion of length 6) and the first
program I wrote took from half a second to three hours to verify them. I found a few interesting
cases in the 154 constructions it did manage to check, including a six step construction that works
for general right triangles. Then I decided to filter the potential constructions by checking
which ones worked on 5 12 13 and 40 13 37 triangles (in addition to the 3 4 5 triangles they are
generated from), but none of them did, which means there are no six step constructions for the
circle tangent to three tangent circles in the general case. I also learned about Coxeter diagrams,
quadratic forms, and Vinberg's algorithm, which constitute a more general method for generating sphere
packings than polyhedral graphs since they work in higher dimensions.
- Week 4:
- Since I found that there were no general six step constructions, I began writing my paper this week. I got a first draft done, wrote up the algorithms, methodolgy, results, and so on. But then on Thursday I discovered that actually an important assumption I made is wrong and the problem is much harder than I thought. Specifically, since the inner Apollonian circle is unique and fully constrained, I assumed that picking arbitrary points would not result in a more efficient construction. It turns out that this isn't true, so I need to figure out how to represent arbitrary points and select them, and determine if it is at all practical to brute force the problem with this added complexity or if it can be simplified. I did some preliminary work coming up with an approach which should be correct but not necessarily tractable involving considering the polyhedral graph associated with all the points and segments and regions in the plane in a geometric construction. It is clear that considering only one point from each 2, 1, and 0 dimensional region in the aformentioned graph is sufficient, and these regions can be thought of as the regions of the plane with respect to pairs of geometric objects. The regions of the plane with respect to single geometric objects up to symmetry are much simpler since then we only have on the object and not on the object as regions, but I'm not sure picking arbitrary points in the regions with respect to single geometric objects up to symmetry is sufficient. We already have at least two points on and one point off of every geometric object in all of the initial configurations for the construction we care about so if this is sufficient that would mean the computation does not need to be changed. I started rewriting the program to allow easier modification to add the graph and support for picking arbitrary points.
- Week 5:
- So far my rewritten version of the program is about up to where the original version was and I am still no closer to getting any nice results about how much symmetry affects arbitrary points. I also considered the coordinates of the center of the inner Apollonian circle, called the inner Soddy center or equal detour point. These coordinates can help us get a lower bound on the number of steps required to do some construction, because only numbers which can be written as expressions involving integers, addition, subtraction, multiplication, division, and square roots can be constructed. These numbers correspond to field extensions of the rational numbers by roots of polynomials. Unfortunately, the polynomials for the Soddy center are quadratic which I believe gives a lower bound of two or four steps which is useless because I might not be able to search five steps deep to show there are no six step constructions with arbitrary points yet, but after three steps I definitely won't have the center of the Apollonian circle and a point on it.
Presentations
Additional Information
- My Mentors
